Ornstein-Uhlenbeck Stochastic Clocks

Posted on by

After introducing the general idea of stochastic clocks in the previous post, we now consider the case where the instantaneous rate of activity follows a non-Gaussian Ornstein-Uhlenbeck process. The major reference is the paper by Barndorff-Nielsen and Shephard (2001b), see also Barndorff-Nielsen and Shephard (2001a). In this post, we discuss the general stochastic setup that applies to all such models that are driven by an almost surely non-decreasing Lévy processes. For the moment, we leave the particular dynamics of this subordinator unspecified but we will provide examples in future posts.

Related Posts

Subordinator Lévy Processes

We start by giving the conditions for a Lévy process to be a subordinator. Let Z = \left\{ Z_t: t \in \mathbb{R}_+ \right\} be a one-dimensional Lévy processes process with characteristic triplet \left( \sigma^2, \nu, \gamma \right). Here, the Radon measure \nu(\mathrm{d}x) on \mathbb{R} \backslash 0 satisfies

    \[ \int_{\mathbb{R} \backslash 0} \left( \vert x \vert^2 \wedge 1 \right) \nu(\mathrm{d}x) < \infty \]

such that the Lévy-Itō decomposition exists, see e.g. Proposition 3.7 in Cont and Tankov (2004). As usual, the characteristic triplet is given w.r.t. the truncation function g(x) = \mathrm{1}_{\{ \vert x \vert \leq 1 \}}. We recall the conditions that the Lévy triplet has to satisfy such that the paths of Z are almost surely non-decreasing. First, for the paths to be of finite variation, they cannot have a Gaussian component, i.e. \sigma = 0, and

    \[ \int_{0 < \vert x \vert \leq 1} \vert x \vert \nu(\mathrm{d}x) < \infty, \]

see e.g. Theorem 21.9 in Sato (1999) or Proposition 3.9 in Cont and Tankov (2004). Second, the jumps of Z need to be non-negative and thus

    \[ \int_{-\infty}^0 \nu(\mathrm{d}x) = 0. \]

Consequently, the Lévy measure satisfies

    \[ \int_0^\infty \left( x \wedge 1 \right) \nu(\mathrm{d}x) < \infty. \]

Now let J_Z(\mathrm{d}t \times \mathrm{d}x) be a Poisson random measure with intensity measure \nu(\mathrm{d}x). Due to the above conditions imposed on the Lévy measure, it is not necessary to compensate for the small jumps and the Lévy-Itō decomposition simplifies to

    \[ Z_t = \left( \gamma - \int_{0 < x \leq 1} x \nu(\mathrm{d}x) \right) t + \int_0^t \int_0^\infty x J_Z(\mathrm{d}u \times \mathrm{d}x). \]

Non-Gaussian Ornstein-Uhlenbeck Process

The instantaneous rate of activity process y = \left\{ y_t: t \in \mathbb{R}_+ \right\} follows a non-Gaussian Ornstein-Uhlenbeck process. It has the dynamics

(1)   \begin{equation*} dy_t = -\lambda y_t \mathrm{d}t + \mathrm{d}Z_{\lambda t} \end{equation*}

subject to y_0 \in \mathbb{R}_+ and where \lambda \in \mathbb{R}_+. Here Z is a subordinator Lévy process as defined in the previous section. It is often referred to as the background driving Lévy process. The definition of y given here is in accordance with the one in Barndorff-Nielsen and Shephard (2001b).

Due to the Z having almost surely non-negative increments, it follows that y is strictly positive. To get some intuition for its paths, assume for the moment that Z follows a compound Poisson process with non-negative jumps. Then the paths of Z are piecewise constant. Now let t \in \mathbb{R}_+ be such that \lambda t is a jump time of Z, then \Delta y_t = \Delta Z_{\lambda t}. Inbetween two jumps, Z is piecewiese constant and thus y is piecewise continuous. It exponentially decays at the rate \lambda.

This general setup encompasses various special cases that have been examined in the literature, such as the gamma and the inverse Gaussian Ornstein-Uhlenbeck processes. These names are not based on, as one might first suspect, the type of process followed by Z but instead on the stationary distribution of y. We analyze these two special cases in later posts. To find the solution to Equation (1), we first find the dynamics of e^{\lambda t} y_t to be

    \[ d \left( e^{\lambda t} y_t \right) = e^{\lambda t} \mathrm{d}Z_{\lambda t} \]

and then integrate both sides to obtain

    \[ y_t = e^{-\lambda t} y_0 + \int_0^t e^{\lambda (u - t)} \mathrm{d}Z_{\lambda u}. \]

It is convenient to make a change of variables by setting v = \lambda u such that

    \[ y_t = e^{-\lambda t} y_0 + \int_0^{\lambda t} e^{v - \lambda t} \mathrm{d}Z_v \]

The total activity process Y = \left\{ Y_t: t \in \mathbb{R}_+ \right\} is then defined as

    \[ Y_t = \int_0^t y_u \mathrm{d}u. \]

Characteristic Function

We are now interested in finding the characteristic function \phi_{Y_t}(\omega) of Y_t. By definition

    \begin{align*} \phi_{Y_t}(\omega) & = \mathbb{E} \left[ e^{\mathrm{i} \omega Y_t} \right]\\ & = \mathbb{E} \left[ \exp \left\{ \mathrm{i} \omega \int_0^t \left( e^{-\lambda u} y_0 + \int_0^{\lambda u} e^{v - \lambda u} \mathrm{d}Z_v \right) \mathrm{d}u \right\} \right]. \end{align*}

We now solve the first of the two integrals in the exponent and reverse the order of integration for the second to get

    \[ \ldots = \mathbb{E} \left[ \left\{ \frac{\mathrm{i} \omega y_0}{\lambda} \left( 1 - e^{-\lambda t} \right) + \mathrm{i} \omega \int_0^{\lambda t} \int_{v / \lambda}^t e^{v - \lambda u} \mathrm{d}u \mathrm{d}Z_v \right\} \right]. \]

Here, we carefully adjusted the limits such that the domain of integration stays unchanged. We now take the first non-random term outside the expectation and solve the inner integral to get

    \[ \ldots = \exp \left\{ \frac{\mathrm{i} \omega y_0}{\lambda} \left( 1 - e^{-\lambda t} \right) \right\} \mathbb{E} \left[ \exp \left\{ \frac{\mathrm{i} \omega}{\lambda} \int_0^{\lambda t} \left( 1 - e^{v - \lambda t} \right) \mathrm{d}Z_v \right\} \right]. \]

To evaluate the remaining expectation, let \Pi = \left\{ t_0 = 0, t_1, \ldots, t_n = \lambda t \right\} be a partition of the interval [0, \lambda t]. Then, not being fully rigorous, we get

    \begin{align*} & \mathbb{E} \left[ \exp \left\{ \frac{\mathrm{i} \omega}{\lambda} \int_0^{\lambda t} \left( 1 - e^{v - \lambda t} \right) \mathrm{d}Z_v \right\} \right]\\ & = \lim_{\vert \vert \Pi \vert \vert \downarrow 0} \mathbb{E} \left[ \exp \left\{ \frac{\mathrm{i} \omega}{\lambda} \sum_{i = 1}^n \left( 1 - e^{t_{i - 1} - \lambda t} \right) \left( Z_{t_i} - Z_{t_{i - 1}} \right) \right\} \right]\\ & = \lim_{\vert \vert \Pi \vert \vert \downarrow 0} \prod_{i = 1}^n \mathbb{E} \left[ \exp \left\{ \frac{\mathrm{i} \omega}{\lambda} \left( 1 - e^{t_{i - 1} - \lambda t} \right) \left( Z_{t_i} - Z_{t_{i - 1}} \right) \right\} \right]. \end{align*}

Here, we used that the increments of the Lévy process Z over non-overlapping time intervals, \hat{Z}_{t_i} - \hat{Z}_{t_{i - 1}}, are pairwise independent. Now denote by \psi_{Z_1}(\omega) the characteristic exponent of the process Z, i.e. it is the logarithm of the characteristic function of Z_1

    \[ \psi_{Z_t}(\omega) = \ln \left( \mathbb{E} \left[ e^{\mathrm{i} \omega Z_t} \right] \right). \]

For the moment, we are not concerned about the particular functional form that \psi_{Z_t}(\omega) takes. Since Z is a Lévy process, it follows that the characteristic function \phi_{Z_t}(\omega) of Z_t can be expressed as

    \[ \phi_{Z_t}(\omega) = \exp \left\{ t \psi_{Z_1}(\omega) \right\}, \]

see e.g. Proposition 3.2 in Cont and Tankov (2004) or Theorem 1.3.3 in Applebaum (2004). Consequently, we can write the last expression as

    \begin{align*} & = \lim_{\vert \vert \Pi \vert \vert \downarrow 0} \prod_{i = 1}^n \exp \left\{ \left( t_i - t_{i - 1} \right) \psi_{Z_1} \left( \frac{\omega}{\lambda} \left( 1 - e^{t_{i - 1} - \lambda t} \right) \right) \right\}\\ & = \lim_{\vert \vert \Pi \vert \vert \downarrow 0} \exp \left\{ \sum_{i = 1}^n \left( t_i - t_{i - 1} \right) \psi_{Z_1} \left( \frac{\omega}{\lambda} \left( 1 - e^{t_{i - 1} - \lambda t} \right) \right) \right\}\\ & = \exp \left\{ \int_0^{\lambda t} \psi_{Z_1} \left( \frac{\omega}{\lambda} \left( 1 - e^{v - \lambda t} \right) \right) \mathrm{d}v \right\}. \end{align*}

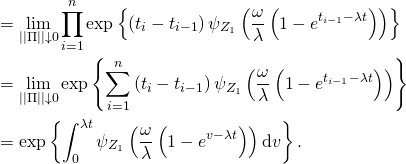
See also Proposition 2.1 in Barndorff-Nielson (2001) and Cont and Tankov (2004) for similar results. By reversing the change of variables and setting u = v / \lambda, we finally obtain

    \[ \phi_{Y_t}(\omega) = \exp \left\{ \frac{\mathrm{i} \omega y_0}{\lambda} \left( 1 - e^{-\lambda t} \right) + \lambda \int_0^{t} \psi_{Z_1} \left( \frac{\omega}{\lambda} \left( 1 - e^{\lambda (u - t)} \right) \right) \mathrm{d}u \right\}. \]

Summary

In this post, we defined the general class of non-Gaussian Ornstein-Uhlenbeck processes that are driven by a subordinator Lévy process. Their characteristic function can be expressed in terms of the characteristic exponent of the background driving Lévy process. To find explicit expressions, we thus need to next impose assumptions on the characteristic triplet (0, \nu, \gamma). This will be the topic of future posts.

References

Applebaum, David (2004) Lévy Processes and Stochastic Calculus: Cambridge University Press

Barndorff-Nielsen, Ole E. (2001) “Superposition of Ornstein-Uhlenbeck Type Processes,” Theory of Probability and its Applications, Vol. 45, No. 2, pp. 175-194

Barndorff-Nielsen, Ole E. and Neil Shephard (2001a) “Modelling by Lévy Processes for Financial Econometrics,” in Ole E. Barndorff-Nielsen, Thomas Mikosch and, and Sidney I. Resnick eds. Lévy Processes – Theory and Applications: Birkhauser, pp. 283-318

———- (2001b) “Non-Gaussian Ornstein Uhlenbeck-based Models and some of their Uses in Financial Economics,” Journal of the Royal Statistical Society – Series B, Vol. 63, NO. 2, pp. 167-241.

Cont, Rama and Tankov, Peter (2004) Financial Modelling with Jump Processes: Chapman & Hall

Sato, Ken-iti (1999) Lévy Processes and infinitely divisible Distributions: Cambridge University Press

Leave a Reply

Your email address will not be published. Required fields are marked *