In quantitative finance, automatic differentiation is commonly used to efficiently compute price sensitivities. See Homescu (2011) for a general introduction and overview. I recently started to look into it with two different applications in mind: i) computation of moments from characteristic functions and ii) computation of implied densities from parametric volatility smiles. In this post, I provide a short introduction into computing general order derivatives with CppAD in forward mode.
There exists a number of other automatic differentiation libraries for C++ which are also very mature and under constant development. I chose CppAD mainly because it supports complex numbers which is important when working with characteristic functions.
General Order Forward Mode
There are two main modes in automatic differentiation: forward and backward. We are concerned with forward mode where one sweep computes the partial derivative of all dependent variables with respect to one independent variable. Consider a function ![]() . We want to evaluate
. We want to evaluate ![]() and its first
and its first ![]() derivatives at the point
derivatives at the point ![]() . Let
. Let
![]()
and define
![]()
Here, ![]() is the function value at
is the function value at ![]() and
and ![]() is related to the corresponding
is related to the corresponding ![]() -th order derivative. The role of the coefficients
-th order derivative. The role of the coefficients ![]() is explained further below. The left hand side evaluates to
is explained further below. The left hand side evaluates to
![]()
The right hand side is obtained by a repeated application of the chain rule. The first four derivatives are given by
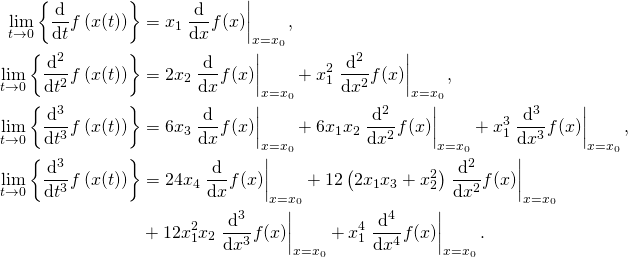
The coefficients ![]() are weights on the derivatives that need to be passed to CppAD. That is, to compute the first order derivative, we set
are weights on the derivatives that need to be passed to CppAD. That is, to compute the first order derivative, we set ![]() and get
and get
![]()
It is easy to show that in order to compute the ![]() -th order derivative, we set
-th order derivative, we set ![]() and
and ![]() for
for ![]() to get
to get
![]()
Code Example
In order to compute the ![]() -th order derivative in forward mode with CppAd, we first create an
-th order derivative in forward mode with CppAd, we first create an ADFun object which stores the operation sequence. We can then iteratively call .Forward(order, scalings) on this function to compute the vector ![]() for the coefficient vector
for the coefficient vector ![]() .
.
// non-standard includes
#include <boost/container/small_vector.hpp>
#include <cppad/cppad.hpp>
// differentiate general function of one variable
template<size_t order, typename Type, typename Function>
small_vector<Type, order + 1> differentiate(Function function,
Type xValue) {
static_assert(order > 0, "Order has to be at least one.");
// setup the mapping / record the sequence
small_vector<AD<Type>, 1> xValue2 { xValue };
Independent(xValue2);
small_vector<AD<Type>, 1> yValue { function(xValue2[0]) };
ADFun<Type> mapping(xValue2, yValue);
// compute all orders at once
small_vector<Type, order + 1> scalings(order + 1);
scalings[0] = xValue;
scalings[1] = Type(1.0);
for (size_t i = 2; i <= order; ++i) {
scalings[i] = Type(0.0);
}
auto result = mapping.Forward(order, scalings);
// scale the results by the Taylor coefficients
double multiplier = 1.0;
for (size_t i = 2; i <= order; ++i) {
multiplier *= static_cast<double>(i);
result[i] *= multiplier;
}
return result;
}
Note that in the above code, we use small_vector form the Boost library instead of an STL vector to avoid heap allocations. While our previous discussion only considered real valued functions of a real variable, the function differentiate(...) has a templated parameter and return value type. Below is a simple test that differentiates a polynomial.
// general polynomial
template<size_t degreePlusOne, typename Type>
Type polynomial(array<double, degreePlusOne> const & coefficients,
Type value) {
Type result(coefficients[0]);
Type power(1.0);
for (size_t i = 1; i < degreePlusOne; ++i) {
power *= value;
result += power * coefficients[i];
}
return result;
}
int main() {
// setup the test function
array<double, 4> coefficients {{ 1.0, 1.0, 1.0, 1.0 }};
auto function = [&](auto value) {
return polynomial(coefficients, value);
};
// take the first four derivatives at x = 1.0
auto derivatives = differentiate<4, double>(function, 1.0);
for (size_t i = 0; i <= 4; ++i) {
cout << i << " -> " << derivatives[i] << endl;
}
}
In the above code, we can simply replace differentiate<4, double> by differentiate<4, complex.
References
Homescu, Cristian (2011) “Adjoints and Automatic (Algorithmic) Differentiation in Computational Finance,” Working Paper, available at SSRN http://ssrn.com/abstract=1828503
