Gamma Ornstein-Uhlenbeck Stochastic Clocks

Posted on by

In this post, we consider one particular specification of the background driving Lévy process in the general Ornstein-Uhlenbeck stochastic clock dynamics introduced in a previous post. We show that a compound Poisson process with exponentially distributed increments yields a gamma stationary distribution for the instantaneous rate of activity. We also discuss how the problem could be approached from the other end by imposing the stationary distribution and finding the corresponding background driving Lévy process.

Related Posts

Construction via the Background Driving Lévy Process

Let

    \[ Z_t = \sum_{i = 1}^{N_t} X_i, \]

where N = \left\{ N_t : t \in \mathbb{R}_{+, 0} \right\} is a Poisson process with arrival rate a \in \mathbb{R}_+ and \left\{ X_i \right\}_{i = 1}^\infty is a sequence of independent identically distributed (i.i.d.) exponential random variables with mean 1 / b for b \in \mathbb{R}_+. See Barndorff-Nielsen and Shephard (2001a) or Chapter 5.2 in Schoutens (2003) for this construction of the gamma Ornstein-Uhlenbeck process. The characteristic function of the background driving Lévy process is given by

    \[ \phi_{Z_t}(\omega) = \exp \left\{ a t \left( \phi_X(\omega) - 1 \right) \right\}, \]

where \phi_{X}(\omega) is

    \[ \phi_X(\omega) = \frac{b}{b - \mathrm{i} \omega}; \]

see e.g. Proposition 3.4 in Cont and Tankov (2004). The corresponding characteristic exponent is thus

    \[ \psi_{Z_1}(\omega) = \frac{\mathrm{i} \omega a}{b - \mathrm{i} \omega}. \]

The characteristic function \phi_y(\omega) of the instantaneous rate of activity is

    \begin{align*} \phi_{y_t}(\omega) & = \mathbb{E} \left[ \exp \left\{ \mathrm{i} \omega y_t \right\} \right]\\ & = \mathbb{E} \left[ \exp \left\{ \mathrm{i} \omega \left( e^{-\lambda t} y_0 + \int_0^{\lambda t} e^{v - \lambda t} \mathrm{d}Z_v \right) \right\} \right]\\ & = \exp \left\{ \mathrm{i} \omega e^{-\lambda t} y_0 + \lambda \int_0^t \psi_{Z_1} \left( \omega e^{\lambda (u - t)} \right) \mathrm{d}u \right\}\\ & = \exp \left\{ \mathrm{i} \omega e^{-\lambda t} y_0 - \left. a \ln \left( b e^{\lambda t} - \mathrm{i} \omega e^{\lambda u} \right) \right|_{u = 0}^{u = t} \right\}\\ & = \exp \left\{ \mathrm{i} \omega e^{-\lambda t} y_0 + a \ln \left( \frac{b - \mathrm{i} \omega e^{-\lambda t}}{b - \mathrm{i} \omega} \right) \right\}. \end{align*}

Here, we used the previously obtained result that links the expected value of an exponential stochastic integral with respect to Z to the exponential integral over the characteristic exponent \phi_{Z_1}(\omega), i.e.

    \[ \mathbb{E} \left[ \exp \left\{ \mathrm{i} \omega \int_0^{\lambda t} e^{v - \lambda t} \mathrm{d}Z_v \right\} \right] = \exp \left\{ \lambda \int_0^t \psi_{Z_1} \left( \omega e^{\lambda (u - t)} \right) \mathrm{d}u \right\}. \]

Taking the limit yields

    \begin{align*} \lim_{t \rightarrow \infty} \phi_{y_t}(\omega) & = \exp \left\{ a \ln \left( \frac{b}{b - \mathrm{i} \omega} \right) \right\}\\ & = \left( \frac{b}{b - \mathrm{i} \omega} \right)^a. \end{align*}

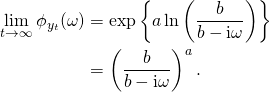
We recognize this as the characteristic function of a \Gamma(a, b) gamma distributed random variable as previously claimed.

Construction via the Stationary Distribution

Without assuming a particular form of the background driving Lévy process Z, we start from

    \[ \phi_{y_t}(\omega) = \exp \left\{ \mathrm{i} \omega e^{-\lambda t} y_0 + \lambda \int_0^t \psi_{Z_1} \left( \omega e^{\lambda (u - t)} \right) \mathrm{d}u \right\} \]

as above. Let

    \begin{align*} \psi_{y_\infty}(\omega) & = \lim_{t \rightarrow \infty} \ln \left( \phi_{y_t}(\omega) \right)\\ & = \lim_{t \rightarrow \infty} \lambda \int_0^t \psi_{Z_1} \left( \omega e^{\lambda (u - t)} \right) \mathrm{d}u \end{align*}

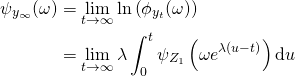
be the cumulant generating function of the stationary distribution of y. Then (not being fully rigorous)

    \begin{align*} \psi_{y_\infty}'(\omega) & = \lim_{t \rightarrow \infty} \lambda \int_0^t \frac{\partial}{\partial \omega} \psi_{Z_1} \left( \omega e^{\lambda (u - t)} \right) \mathrm{d}u\\ & = \lim_{t \rightarrow \infty} \lambda \int_0^t \psi_{Z_1}' \left( \omega e^{\lambda (u - t)} \right) e^{\lambda (u - t)} \mathrm{d}u\\ & = \left. \lim_{t \rightarrow \infty} \frac{1}{\omega} \psi_{Z_1} \left( \omega e^{\lambda (u - t)} \right) \right|_{u = 0}^{u = t}\\ & = \left. \lim_{t \rightarrow \infty} \frac{1}{\omega} \left( \psi_{Z_1}(\omega) - \psi_{Z_1} \left( \omega e^{-\lambda t} \right) \right)\\ & = \frac{1}{\omega} \psi_{Z_1}(\omega). \end{align*}

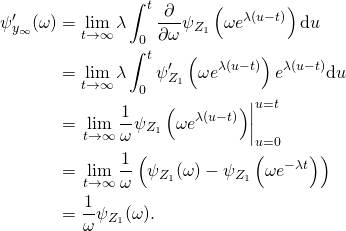
This relationship between the cumulant generating function of the stationary distribution of y_t and the cumulant generating function of the background driving Lévy process has been obtained by Barndorff-Nielsen (2001). Now, given that the stationary distribution of y is \Gamma(a, b) with

    \[ \psi_{y_\infty}(\omega) = a \ln \left( \frac{b}{b - \mathrm{i} \omega} \right) \]

we get

    \begin{align*} \psi_{Z_1}(\omega) & = w \psi_{y_\infty}'(\omega)\\ & = \frac{\mathrm{i} a \omega}{b - \mathrm{i} \omega}. \end{align*}

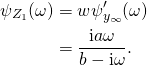
As shown before, this is the cumulant generating function of a compound Poisson process with arrival rate a and i.i.d. exponentially distributed increments with mean 1 / b.

Integrated Time-Change

As shown in my previous post, the general solution for the characteristic function of the total activity process Y = \left\{ Y_t : \mathbb{R}_{+, 0} \right\} is given by

    \[ \phi_{Y_t}(\omega) = \exp \left\{ \frac{\mathrm{i} \omega y_0}{\lambda} \left( 1 - e^{-\lambda t} \right) + \lambda \int_0^t \psi_{Z_1} \left( \frac{\omega}{\lambda} \left( 1 - e^{\lambda (u - t)} \right) \right) \mathrm{d}u \right\}. \]

The integral evaluates to

    \begin{align*} \ldots & = \lambda \int_0^{t} \psi_{Z_1} \left( \frac{\omega}{\lambda} \left( 1 - e^{\lambda (u - t)} \right) \right) \mathrm{d}u\\ & = \int_0^t \frac{\mathrm{i} \omega a \lambda }{b \lambda \left( 1 - e^{\lambda (u - t)} \right) - \mathrm{i} \omega} \mathrm{d}u\\ & = \left. \frac{a \lambda}{\mathrm{i} \omega - b \lambda} \left( b \ln \left( b \lambda - \left( 1 - e^{\lambda (u - t)} \right) \mathrm{i} \omega \right) - \mathrm{i} \omega u \right) \right|_{u = 0}^{u = t}\\ & = \frac{a \lambda}{\mathrm{i} \omega - b \lambda} \left( b \ln \left( \frac{b \lambda}{b \lambda - \mathrm{i} \omega \left( 1 - e^{-\lambda t} \right)} \right) - \mathrm{i} \omega t \right). \end{align*}

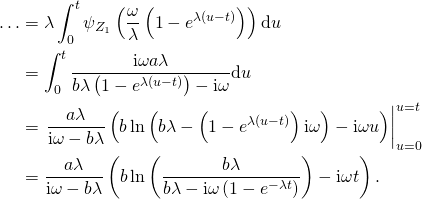
Putting everything together, we get

    \[ \phi_{Y_t}(\omega) = \exp \left\{ \frac{\mathrm{i} \omega y_0}{\lambda} \left( 1 - e^{-\lambda t} \right) + \frac{a \lambda}{\mathrm{i} \omega - b \lambda} \left( b \ln \left( \frac{b \lambda}{b \lambda - \mathrm{i} \omega \left( 1 - e^{-\lambda t} \right)} \right) - \mathrm{i} \omega t \right) \right\}. \]

This coincides with the expression given in Chapter 7.2 of Schoutens (2003).

References

Barndorff-Nielsen, Ole E. (2001) “Superposition of Ornstein-Uhlenbeck Type Processes,” Theory of Probability and its Applications, Vol. 45, No. 2, pp. 175-194

Barndorff-Nielsen, Ole E. and Neil Shephard (2001a) “Modelling by Lévy Processes for Financial Econometrics,” in Ole E. Barndorff-Nielsen, Thomas Mikosch and, and Sidney I. Resnick eds. Lévy Processes – Theory and Applications: Birkhauser, pp. 283-318

Cont, Rama and Peter Tankov (2004) Financial Modelling with Jump Processes: Chapman & Hall

Schotens, Wim (2003) Lévy Processes in Finance: John Wiley & Sons

Leave a Reply

Your email address will not be published. Required fields are marked *